Feature selection via L1 regularization penalty, greedily removing least impactful features and random forests
Wrapped up Chapter 4 of Python Machine Learning today which covered selecting meaningful features. Note that feature selection is distinct from feature extraction as the author describes.
Using feature selection, we select a subset of the original features. In feature extraction, we derive information from the feature set to construct a new feature subspace.
Reducing the number of features can help combat overfitting, and also improve the performance of a model. Plus, we may get all the way down to 2 or 3 dimensions, where we can visualize the dataset graphically.
L1 vs L2 penalty for feature selection
As previously reviewed, overfitting can be detected when the predictive performance of a trained model is worse on the training dataset than on an unseen test dataset. One technique to combat this mentioned earlier is 'regularization' where an additional parameter is added to the cost function used during training that is the sum of the squares of the weights of the model. This means, all else being equal, we would like our weights to be smaller. Smaller weights have a lower chance of stretching the model to overfit the dataset it was trained on.
Using the sum of the squared weights is called L2 regularization. If we simply sum the absolute values, we're using L1 regularization. For reasons the author does a pretty good job of explaining, using L1 regularization, in addition to shrinking the parameters, also tends to send some parameters down to zero faster than others, effectively eliminating some parameters from the model, or selecting a subset of features.
So: long story short, if you'd like to reduce the number of features at play in your model, and not just shrink them, using an L1 penalty for regularization (available in LogisticRegression) can do the job.
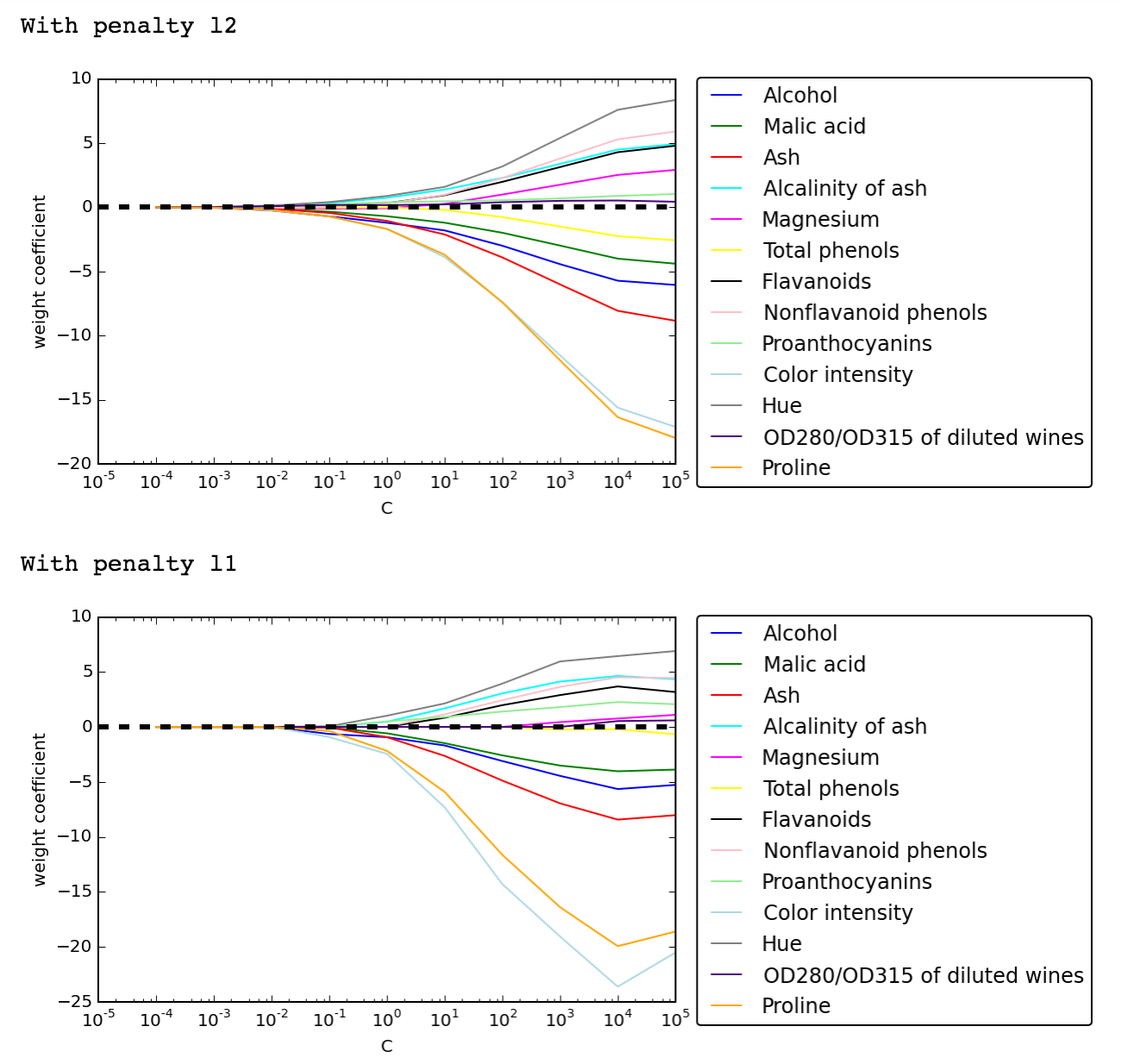
Here are two graphs of how the weights are affected by regularization parameters in L2 and L1 regularization:
(The book had shown just the L1 case, but I thought it'd be interesting to see both for comparison). Note that with l1 penalty, some of the features drop out more quickly than others, e.g 'magnesium' is down to zero as C gets to 10^4.
Sequential feature selection
Another technique to remove features is to try removing each one and see which has the least impact on the performance against the training / test set. This can be repeated until you are down to the number of features you'd like, or the performance suffers too much.
The book implements this approach but it's pretty straightforward so I'll leave it at that.
Random forests' insights into feature importance
Remember that decision trees work by dividing and conquering the training data by splitting on feature thresholds at each level. It may determine, for instance, that the way to maximize the difference in entropy between two levels in a tree is to have one leaf handle every row where sex is 'male' and the other where sex is 'female'.
So you can imagine that as part of this process, a decision tree is in effect learning what the most decisive features are, and as such, scikit-learn's random forest classifier makes this available via the .feature_importances_ attribute of the model.
The book warns
... the random forest technique comes with an important gotcha that is worth mentioning... if two or more features are highly correlated, one feature may be ranked very highly while the information of the other feature(s) may not be fully captured. On the other hand, we don't need to be concerned about this problem if we are merely interested in the predictive performance of a model rather than the interpretation of feature importances.