Random Variables again, regularization to combat high variance and a tour of some classifiers Scikit-learn (SVMs, Decision Trees)
Morning probability warmup
Watched a couple more math monk videos and got caught up for a second on the definition of a random variable as it pertains to measure theory (at this spot in the video). It corresponds to what the All of Stats book notes,
Recall that a probability measure is defined on a $\sigma$-algebra $\mathcal{A}$ of a sample space $\Omega$. A random variable $X$ is a measurable map $X: \Omega \rightarrow \Bbb R$. Measurable means that, for every $x, \{\omega: X(\omega) \leq x\} \in \mathcal{A}$.
Googling around unearthed this concise yet rigorous overview of probability that helped.
Random Variables are useful because they map outcomes of a sample space to real numbers, so that probabilities on this sample space can be defined in terms of the Borel sigma algebra. Specifically, a random variable $X(\omega)$ is a mapping that assigns a real number to each outcome $\omega$ of the sample space $\Omega$. Then we can talk about the probability of events of the form $\{\omega \mid X(\omega) \leq x\}$, where $x$ is a given real number, by using a probability measure defined over the interval $(-\infty, x]$, an interval that falls within the Borel sigma algebra.This probability value, viewed as a function of $x$, is called the cumulative distribution function for $X$ and is usually denoted as $F_x(x)$.
So essentially a random variable must be measurable, as evidence by the existence of a cumulative distribution function. Ahh random variables, such a joy to continuously try to Grok. Also note that in practice, most naturally occurring random variables are measurable, so these technical details about a measurable function aren't really that important.
I've added this to the ml curriculum page.
Regularization to combat overfitting
One topic chapter 3 of Python Machine Learning covers is regularization, a technique used to combat overfitting data.
When a model overfits the data it has been trained on, it has "high variance". It's called "variance" because you can imagine that if you trained the model on different samples of a larger dataset, the weights would vary quite a bit as it overfit whatever it was trained on. Overfitting is bad because it means a model is unlikely to generalize and accurately fit / predict unseen data. (Note: the opposite problem where a model fails to fit the data at all is "high bias").
Regularization can help combat overfitting by penalizing large weights, and this is accomplished by adding this parameter to the cost function:
$$\lambda \sum_{i=1}^n w_i^2$$
Chapter 3 of Python Machine Learning covers this briefly, though I think the choice of example with logistic regression wasn't the best, since it doesn't actually correspond to a bias / variance tradeoff.
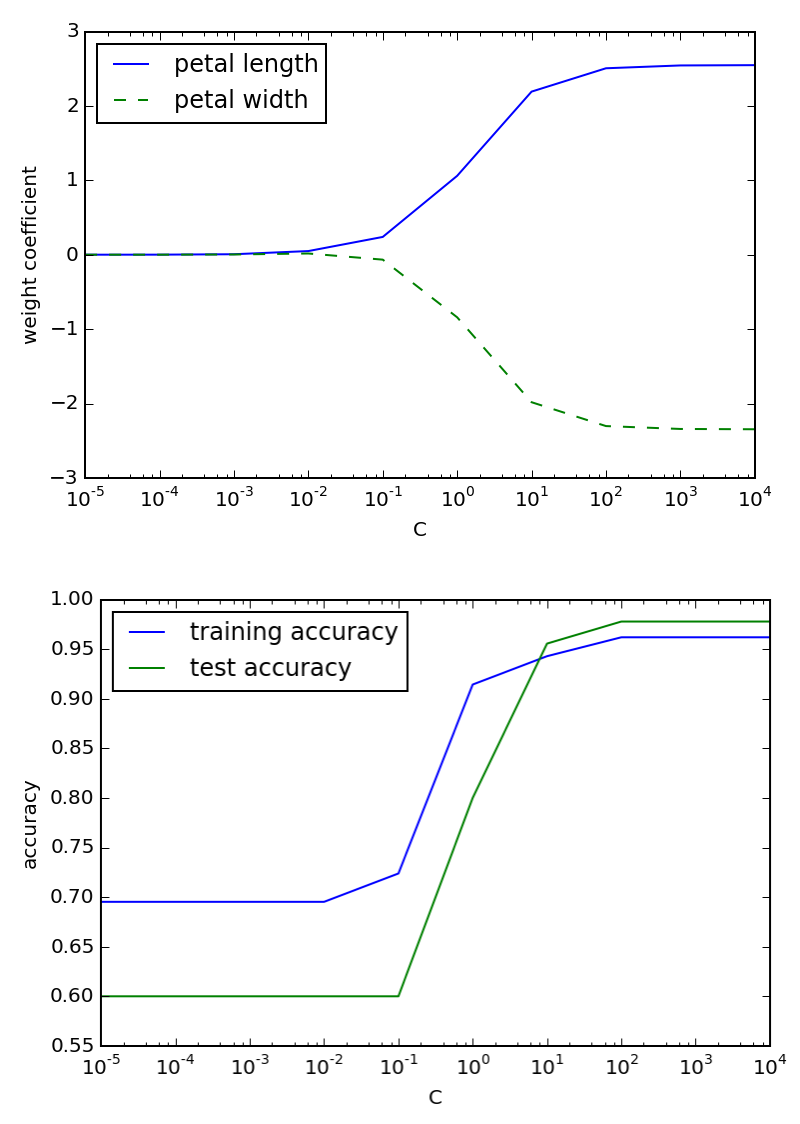
The book showed how the parameters are allowed to get larger when the regularization parameter $C$ increases (which is the inverse of $\lambda$, so the regularization effect is decreasing), but as you can see in the second graph I created, both the training and test accuracy get better, so this is't really a great use case.
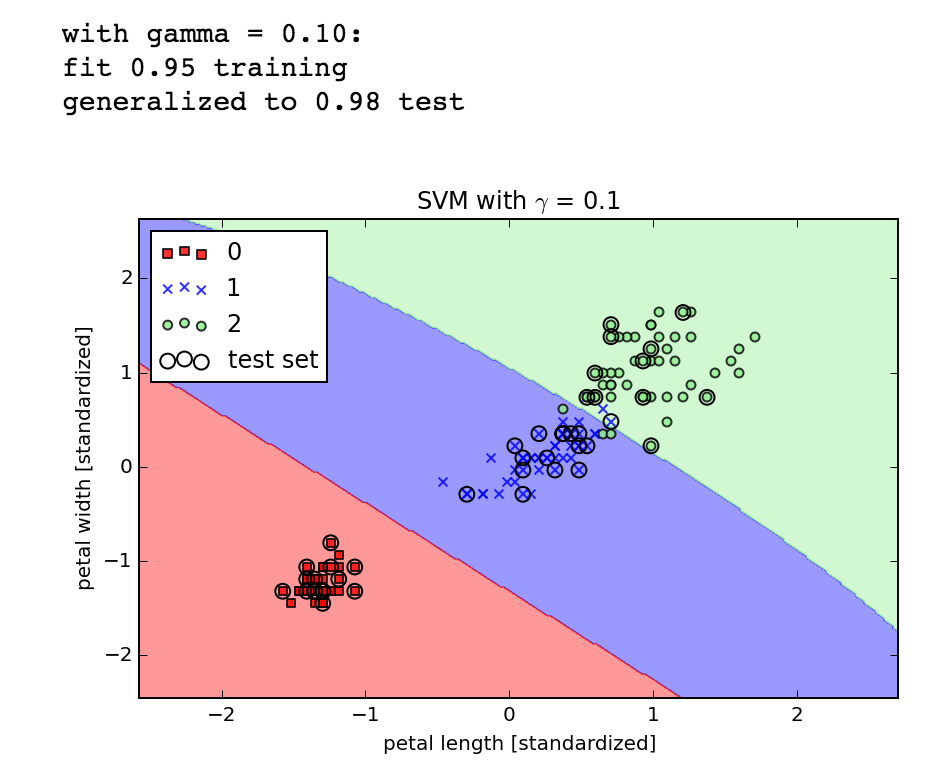
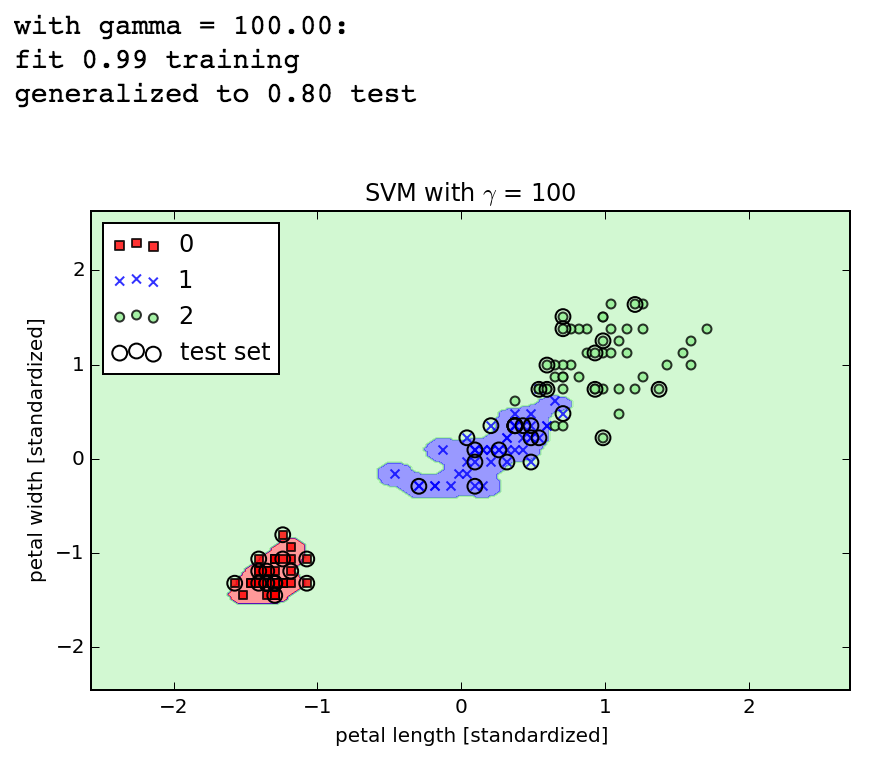
Later, when tuning $\gamma$ with SVMs we show how increasing the parameter too much actually does lead to overfitting, which corresponds to excellent training fit but poorer test fit.
SVMs
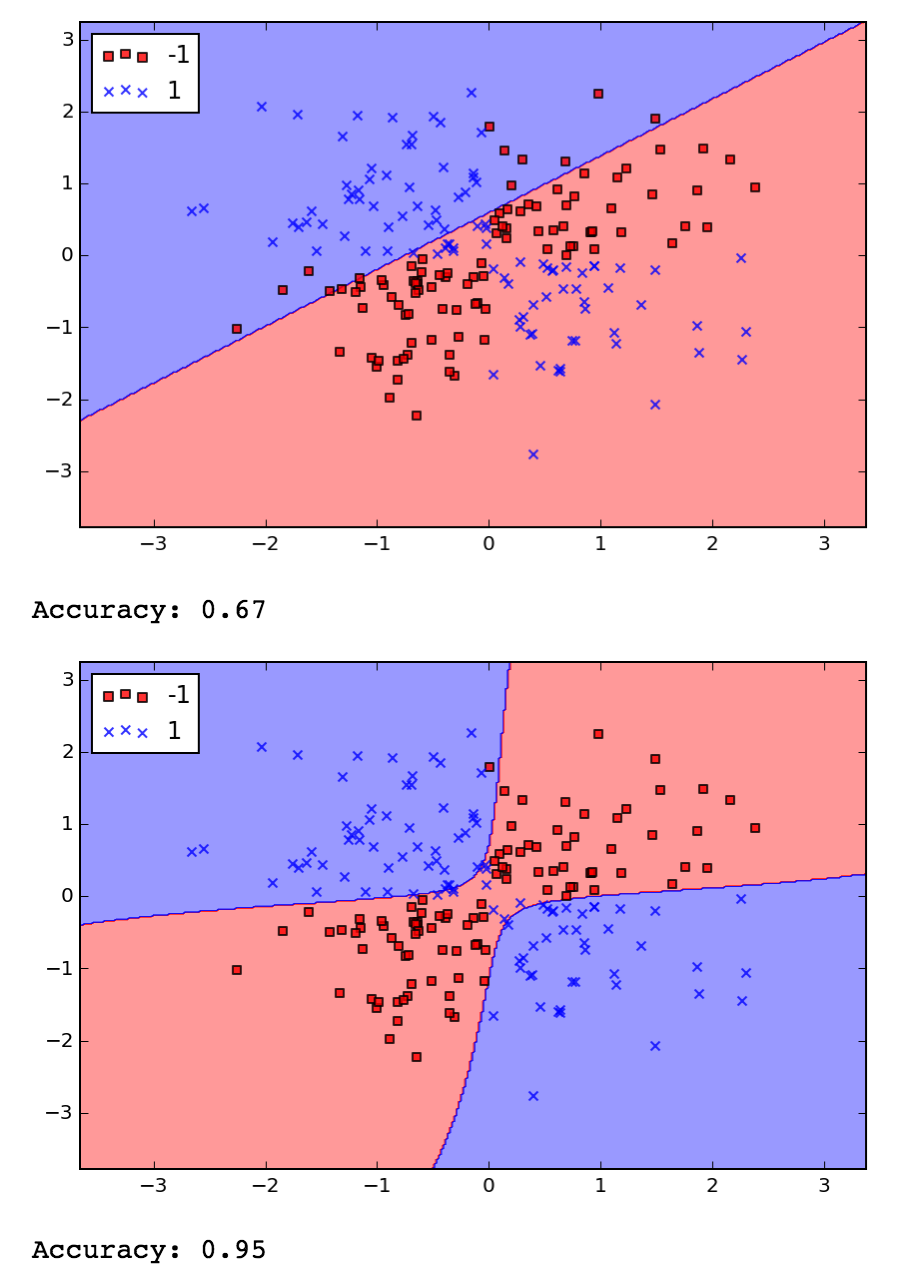
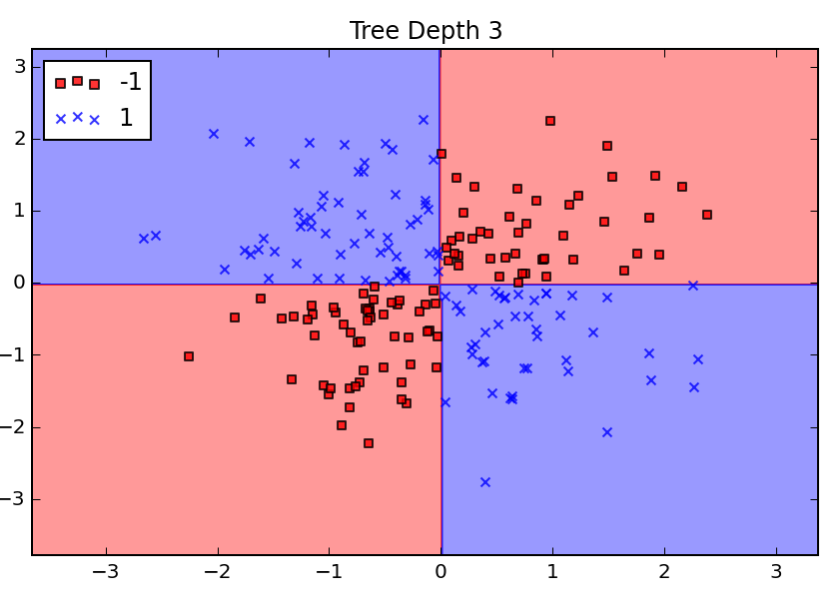
Speaking of SVMs, the book briefly covers support vector machines in chapter 3. I get the big idea that instead of optimizing across all points when attempting to separate the classes of data, you are focusing on the points near the boundary, maximizing the margins, but the book doesn't go into enough theory to really derive the implementation. That's fine for now, it's just cool to see how easy it is to pass in the same data sets into different algorithms using scikit-learn. It was also cool to see the kernel trick in action, where by transforming a dataset a previously linearly inseparable data set becomes separable with the same algorithm. Here's the same XOR dataset separated by SVMs with a linear and then a Gaussian kernel:
Decision Trees
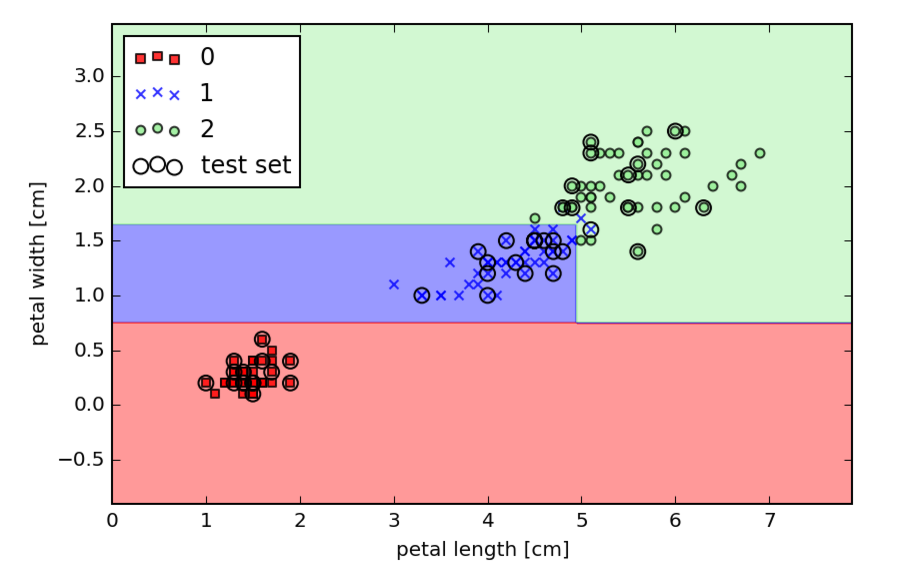
Decision trees are cool. The learning algorithm automatically constructs a binary decision tree where the class membership is determined at the leaves. Decision trees can fit nonlinearly separable data sets and have the added bonus that the models are themselves interpretable by humans.
The trouble with decision trees are that they can overfit the data. This can be mitigated by limiting their depth.
One of the most popular and powerful "ensemble learning" techniques is to combine multiple decision trees that together vote on class membership (random forests). This tends to make the model more robust against overfitting and improve accuracy to boot. The trees tend to cancel each other's overfitting problems so that less tuning is required when training the model. Each tree in the forest looks at a random subset of features and a random sample of the data.
Building a tree: maximizing information gain
The book does a nice job at concisely describing how the learning process works: by maximizing the information gain between levels in the tree. Information gain is quantified by a difference in "impurity". A node where every element belongs to the same class is perfectly pure, and a node where the data is evenly distributed across all classes is perfectly impure, so you can imagine that if you progressively sort the data into nodes where they are grouped together by class, you have built a tree that can help you classify.
The three measures of impurity the book covers are Gini index, entropy and classification error. I won't bother rehashing it here beyond a quick example of how the Gini index is defined:
$$\sum_{i=1}^{c} p(i \mid t)(-p(i \mid t)) = 1 - \sum_{i=1}^{c} p(i \mid t)^2$$
where $p(i \mid t)$ is the proportion of samples that belong to a class $c$ for a node $t$. So the impurity is maximized when there are more classes present in the samples and minimized if they all belong to the same class.
Playing with scikit
The book runs through training the same dataset using scikit-learn's decision tree and random forest learner. Very cool to see how easy this is.
As a bonus, I also explored the overfitting balance with tree depth, where I couldn't really get a single decision tree to overfit the iris dataset that's used across chapter 3, and applied the random forest classifier to the xor dataset: