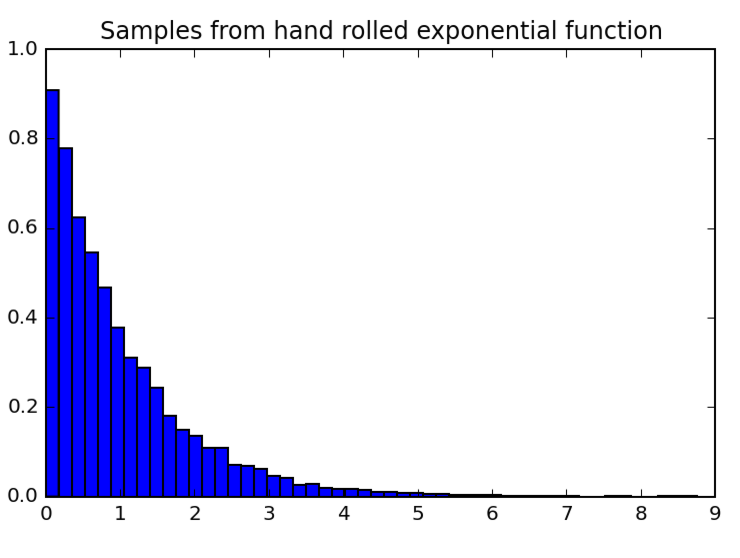
A notebook on inverse transform sampling
Inverse Transform Sampling
In continuing to study the transformation of random variables, I had a bit of an aha moment in understanding the significance of a result I proved in this homework problem
Let $F$ be a CDF, and $U$ a random variable uniformly distributed on $[0, 1]$. Then $F^{-1}(U)$ is a random variable with CDF $F$.
The implication is that we can use the inverse CDF function of any random variable and combine it with a (uniform) random number generator to make a random number generator that adheres to its distribution. This is known as "inverse transform sampling". I wrote up a notebook attempting to tie together the math with some code to make the concept stick.