Probability Density Function hw problem and more math monk vids on conditional probability and indpendance
I ended up spending the entire day on probability theory, starting with problem 4 from chapter 2 that did some stuff with probability distribution functions and cumulative distribution functions. I've fully wrapped up chapter 1 material now, having completed all of the problems from both CMU courses from chapter 1 or related material and have transcribed all of the chapter 2 problems in the homework section so it's easy to kick off each day with some probability homework. I've found morning is much better for that sort of work. The only challenge is in not ending up spending the whole day on it, starving the ML work, like happened today :)
Today's homework problem has two parts, the first pretty straight forward, integrating the PDF to get the CDF, but the second part was really tricky. I had to look at the solution to know where to start, but it was helpful to carefully work through it.
The problem is:
Let $Y = 1/X$. Find the probability density function $f_y(y)$ for $Y$.
I didn't really know where to begin, it seems strange to express one random variable in terms of another. But after peeking, I could see it was a matter of using the definition of what a CDF is and plugging in $1/X$ directly like so:
$F_Y(y) = P(Y \leq y)$ = $P(\frac{1}{X} \leq y)$ = $P(\frac{1}{y} < X)$ = $1 - P(X \leq \frac{1}{y})$
= $1 - F_X(\frac{1}{y})$.
From there it was a matter of plugging and chugging, and using a trick where you can take the reciprocal of both sides of an inequality and flip the inequality sign to manipulate to a clean version of $F_Y(y)$ and then finally taking the derivative to get $f_Y(y)$.
As far as looking at solutions: I really don't have much choice when I'm totally stuck given I'm doing this solo, but I figure taking just enough of a peek to get me over the hump when necessary is similar to going to office hours and getting hints and/or working with other students. And before I do that I re-read relevant sections of the book and google around too, sometimes I can get unstuck but today I really didn't know where to begin without the peek.
Math Monk on independence
Now that I'm into chapter 2 material in problem sets, I figured I should catch up on the mathematical monk probability primer playlist while I was at it, and watched a few more today, including a final review of measure theory, conditional probability and independence.
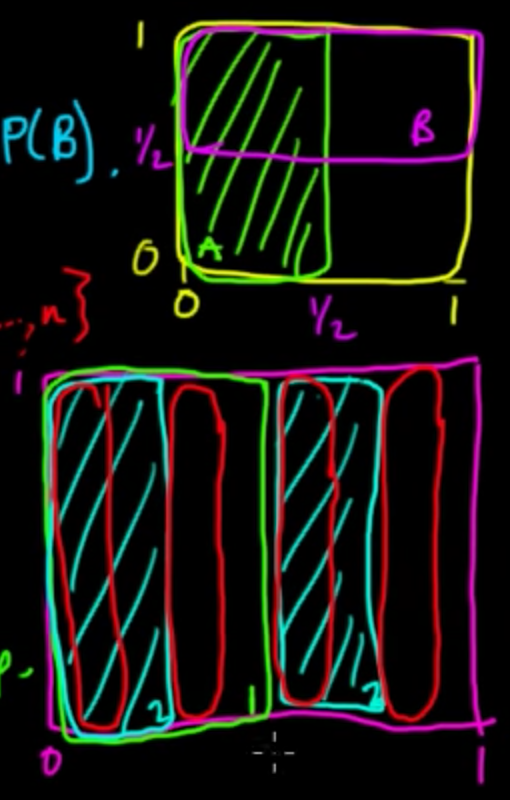
Independence is a funny concept and not really as intuitive as you might think. For instance, disjoint events are not independent because they violate the definition of independence $P(A \cap B) = P(A)P(B)$; each event has non-zero probability but the probability of their intersection is zero. Here's a screenshot of math monk's drawings of independent events:
The top box is two independent events, the bottom 3 independent events.
Sometimes events are just assumed to be independent, like in the case of tossing coins; the first toss has no way of influencing the next, so we assume each toss is an independent event.
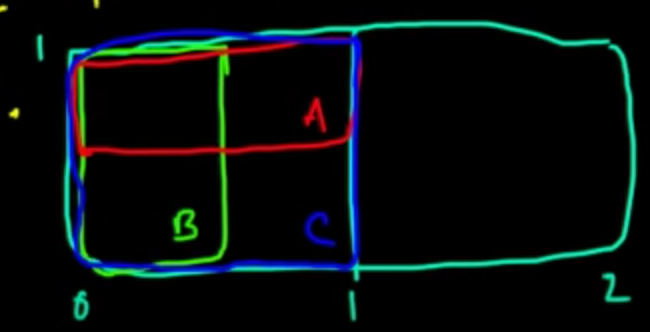
Here's another example using conditional independence where $A$ and $B$ are conditionally independent given $C$, but not independent in general (within the entire sample space $\Omega$). Conditional probability creates a smaller sample space within which you can test for independence.
The definition of conditional independence:
$P(A \cap B \mid C) = P(A \mid C)P(B \mid C)$
A little example problem was proposed in the video that I've worked out here.