Problem
Let $(X, Y)$ have the uniform distribution on the triangle area with vertices (0, 0), (0, 1), and (1, 0). Find the joint density function of $(X, Y)$.
Solution
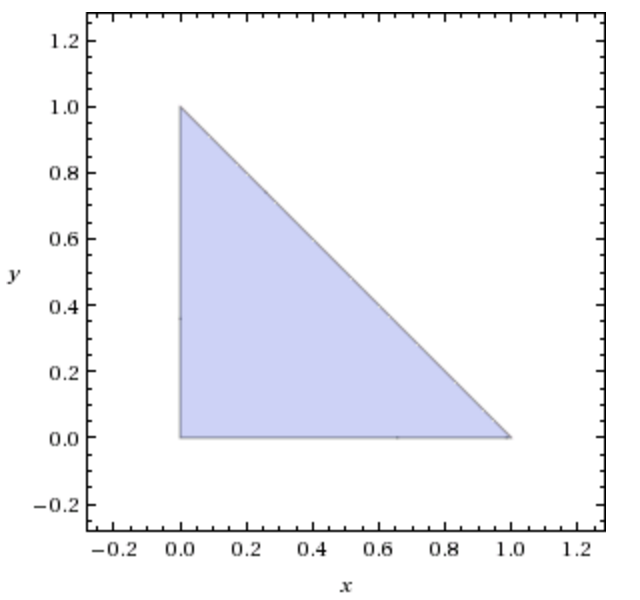
The region of the uniform distribution is the region beneath the function $Y = 1 - X$:
We can describe the joint density function:
$f_{X,Y}(x,y) = \begin{cases} c & 0 \leq x \leq 1, 0 \leq y \leq 1-x \\ 0 & \text{otherwise} \end{cases} $
To solve $c$ we need to ensure that integrating over the entire density gets us 1:
$\int_0^{1} \int_0^{1 - x} c dy dx = 1$
$\int_0^{1} c(1 - x) dx = 1$
$c(x - \frac{x^2}{2}) \rvert_{0}^{1} = 1$
$c(1 - \frac{1}{2}) = 1$
$\frac{c}{2} = 1$
$c = 2$
making our PDF:
$f_{X,Y}(x,y) = \begin{cases} 2 & 0 \leq x \leq 1, 0 \leq y \leq 1-x \\ 0 & \text{otherwise} \end{cases} $
Sources
- 36-700 hw2 problem 6